Espirais n-dimensionais Graceli, com fluxos variados para os lados.
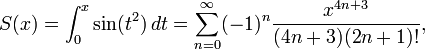 /
/ 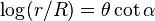 /logΦ/Φ [n]
/logΦ/Φ [n]
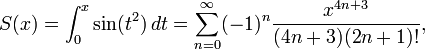 /
/ 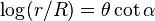 /logΦ/Φ [n]
/logΦ/Φ [n] /
/ 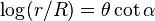 / /logΦ/Φ [n] / t
/ /logΦ/Φ [n] / t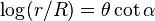 /logΦ/Φ [n]
/logΦ/Φ [n]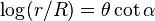 / log Φ / Φ * pP [N]
/ log Φ / Φ * pP [N]
sino quadrimensional Graceli.
2 2 2
- [logx/x -b][n] / 2 logc / c[n] / 2 logΦ/Φ [n]
f [x] = log a /a * [a, R,0][n]
Φ = com o fluxo pelo tempo para os lados do sino temos um sino sequencial em relação ao log, e temos em relação ao fluxo [Φ] um sino quadrimensional com movimentos de fluxos variados.
2 2 2
- [logx/x -b][n] / 2 logc / c[n] / 2 logΦ/Φ [n]
f [x] = log a /a * [a, R,0][n]
Φ = com o fluxo pelo tempo para os lados do sino temos um sino sequencial em relação ao log, e temos em relação ao fluxo [Φ] um sino quadrimensional com movimentos de fluxos variados.
com a alternância de [R,0] o sino desaparece quando multiplicado por zero, e reaparece quando multiplicado por R.
Nenhum comentário:
Postar um comentário